


Next: About this
document ...
Up: GLESP
Description and Examples
Previous: ntot
Description
rsalm convolves the map with a
symmetric beam via
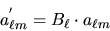 |
(6) |
, where 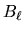 is the expansion in Legendre
polynomials of a symmetric beam.
The symmetric beam can be input by reading in an ASCII file
containing the profile of
is the expansion in Legendre
polynomials of a symmetric beam.
The symmetric beam can be input by reading in an ASCII file
containing the profile of 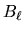 , or by providing the
FWHM for
a symmetric Gaussian beam, where
, or by providing the
FWHM for
a symmetric Gaussian beam, where
![\begin{displaymath}
B_{{\ell}}= \exp[- \sigma^2 {\ell}({\ell}+1) / 2 ]
\end{displaymath}](img42.png) |
(7) |
and
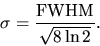 |
(8) |
For deconvolution, a simple Tikhonov regularization scheme is always
applied via
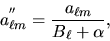 |
(9) |
where 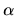 is the regularization parameter.
is the regularization parameter.
Examples
- Convolution:
- De-convolution with Tikhonov regularization:



Next: About this
document ...
Up: GLESP
Description and Examples
Previous: ntot
Gauss Legendre Sky Pixelization