


Next: cmap
Up: GLESP
Description and Examples
Previous: alm2dl
Description
cl2map synthesizes CMB
temperature maps from spherical harmonic coefficients 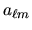 .
.
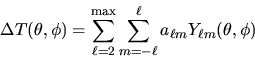 |
(3) |
Inversely,
cl2map
can decompose an input CMB temperature map into its spherical harmonic
coefficients 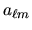 and/or power spectrum:
and/or power spectrum:
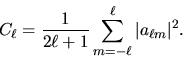 |
(4) |
 |
(5) |
where 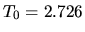 K. If necessary, dipole can be
calculated and included.
K. If necessary, dipole can be
calculated and included.
To synthesize a map,
cl2map
can process an 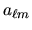 file either in FITS Binary
Extension-like or in
ASCII format, or can process ASCII
file either in FITS Binary
Extension-like or in
ASCII format, or can process ASCII 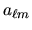 strings.
strings.
If the input is a power spectrum 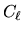 or
or 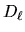 , cl2map
generates a Gaussian map of CMB anisotropies by assigning the
, cl2map
generates a Gaussian map of CMB anisotropies by assigning the 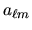 = COMPLEX(
= COMPLEX(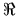 ,
, 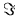 )
mutually independent Gaussian-distributed real (
)
mutually independent Gaussian-distributed real (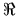 ) and
imaginary part (
) and
imaginary part (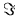 ), both with a standard deviation
), both with a standard deviation
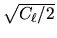 at each
at each 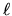 harmonic.
harmonic.
To decompose an input map for its 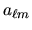 coefficients, cl2map processes
the FITS Binary map with position and temperature
coefficients, cl2map processes
the FITS Binary map with position and temperature
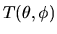 with 3 sections:
with 3 sections:
-
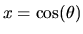 ,
the center-position of the
rings as a function of the polar angle (nx positions),
,
the center-position of the
rings as a function of the polar angle (nx positions),
- nx numbers with the number of pixels, nphi, in the corresponding
ring,
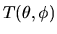 organized
in one row using Point 1 as the major index and Point 2 as
the minor index.
organized
in one row using Point 1 as the major index and Point 2 as
the minor index.
Examples
- Synthesizing a map from given spherical harmonic coefficients:
- cl2map -falm alm.fits -o map.fits
-nx
250 -np 500 -lmax 100
synthesizes the map from input FITS file ' alm.fits'
and outputs to
the
file ' map.fits' with resolution
(250,500). The maximum multipole
number 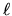 is 100.
is 100.
- cl2map -alm "2,1,1,0" -o
map.y21.fits -nx 100 -np 200 -lmax 4
synthesizes a map from the 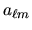 string ' "2,1,1,0"' (
string ' "2,1,1,0"' ( 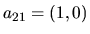 )and outputs to the
file ' map.y21.fits'. The
resolution of the map is (100,200). The maximum multipole number
)and outputs to the
file ' map.y21.fits'. The
resolution of the map is (100,200). The maximum multipole number 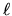 is 4.
is 4.
- cl2map -falm alm.txt -dipole -o
map.dipole.fits -nx 50 -np 100 -lmax 10
synthesizes the dipole map from the input ASCII file ' alm.txt' and
outputs to the file ' map.dipole.fits'.
The
resolution of this dipole
map is (50, 100).
- cl2map -falm alm.fits -di+ -o
map.dip.fits -lmax 50
synthesizes the map (up to 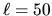 including the dipole)
from the input FITS file ' alm.fits'
and
outputs to the file ' map.dip.fits'.
The
resolution of the map is the
default value, i.e. (201,402).
including the dipole)
from the input FITS file ' alm.fits'
and
outputs to the file ' map.dip.fits'.
The
resolution of the map is the
default value, i.e. (201,402).
- cl2map -falm alm.fits -lmin 5 -lmax
5 -o map.fits
synthesizes the map for 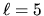 from the input FITS file
' alm.fits' and
outputs to the file ' map.fits'.
The resolution
is the default value (201,402).
from the input FITS file
' alm.fits' and
outputs to the file ' map.fits'.
The resolution
is the default value (201,402).
- cl2map -falm alm.fits -mmin 2 -mmax
10 -nx 400 -np 800 -o map.fits -lmax 50
synthesizes the map up to 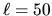 for all
for all 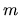 from
2 to 10 from the input
FITS file ' alm.fits' and
outputs to
the file ' map.fits'. The
resolution
is (400,800).
from
2 to 10 from the input
FITS file ' alm.fits' and
outputs to
the file ' map.fits'. The
resolution
is (400,800).
- Gaussian random map simulation from a given angular power
spectrum:
- Map decomposition for its angular power spectrum and/or spherical
harmonic coefficients:



Next: cmap
Up: GLESP
Description and Examples
Previous: alm2dl
Gauss Legendre Sky Pixelization
![]() .
.
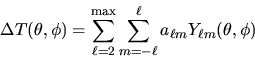
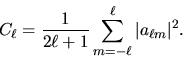
![]() K. If necessary, dipole can be
calculated and included.
K. If necessary, dipole can be
calculated and included.
![]() file either in FITS Binary
Extension-like or in
ASCII format, or can process ASCII
file either in FITS Binary
Extension-like or in
ASCII format, or can process ASCII ![]() strings.
strings.
![]() or
or ![]() , cl2map
generates a Gaussian map of CMB anisotropies by assigning the
, cl2map
generates a Gaussian map of CMB anisotropies by assigning the ![]() = COMPLEX(
= COMPLEX(![]() ,
, ![]() )
mutually independent Gaussian-distributed real (
)
mutually independent Gaussian-distributed real (![]() ) and
imaginary part (
) and
imaginary part (![]() ), both with a standard deviation
), both with a standard deviation
![]() at each
at each ![]() harmonic.
harmonic.
![]() coefficients, cl2map processes
the FITS Binary map with position and temperature
coefficients, cl2map processes
the FITS Binary map with position and temperature
![]() with 3 sections:
with 3 sections: