


Next: rsalm
Up: GLESP Description and Examples
Previous: polmap
description
polalm
decomposes an input CMB temperature map into its spherical harmonic
coefficients 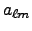 and/or power spectrum:
and/or power spectrum:
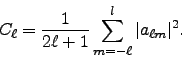 |
(12) |
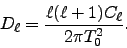 |
(13) |
where 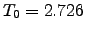 K.
and
calculates decomposition coefficients of scalar and pseudoscalar
potentials (E and B-modes) for Q and U-maps:
K.
and
calculates decomposition coefficients of scalar and pseudoscalar
potentials (E and B-modes) for Q and U-maps:
![\begin{displaymath}
s_{lm}^c=\int_{-1}^1dx[\Phi^m_l(x)U_s^m(x)+F^m_l(x)Q_c^m(x)] ,
\end{displaymath}](img64.png) |
(14) |
![\begin{displaymath}
s^s_{lm}=\int_{-1}^1dx[\Phi^m_l(x)U_c^m(x)-F^m_l(x)Q_s^m(x)] ,
\end{displaymath}](img65.png) |
(15) |
![\begin{displaymath}
p_{lm}^c=\int_{-1}^1dx[F^m_l(x)U_c^m(x)-\Phi^m_l(x)Q_s^m(x)] ,
\end{displaymath}](img66.png) |
(16) |
![\begin{displaymath}
p^s_{lm}=\int_{-1}^1dx[-F^m_l(x)U_s^m(x)-\Phi^m_l(x)Q_c^m(x)] ,
\end{displaymath}](img67.png) |
(17) |
where
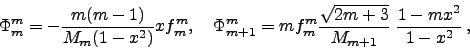 |
(18) |
See other details in the correpsnoding paper of GLESP 2.0.
To decompose an input maps for harmonic coefficients, polalm
processes the FITS Binary map with position and temperature, or Q and U
Stokes parameters
(
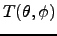 ,
,
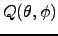 ,
,
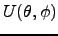 )
in 3 sections:
)
in 3 sections:
-
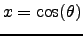 , the center-position of the rings as a function of
the polar angle (nx positions),
, the center-position of the rings as a function of
the polar angle (nx positions),
- nx numbers with the number of pixels, nphi, in the corresponding
ring,
-
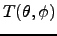 organized in one row using Point 1 as the major index
and Point 2 as the minor index.
organized in one row using Point 1 as the major index
and Point 2 as the minor index.
Examples
- Map decomposition for its angular power spectrum and/or
spherical harmonic coefficients (-map):



Next: rsalm
Up: GLESP Description and Examples
Previous: polmap
Verkhodanov Oleg
2009-04-01
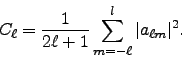
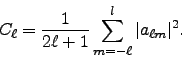
![]() ,
,
![]() ,
,
![]() )
in 3 sections:
)
in 3 sections: